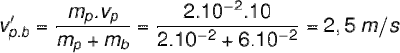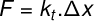1. Seorang anak berjalan lurus satu meter ke barat, kemudian belok ke selatan sejauh 3 meter, dan belok lagi ke timur sejauh 5 meter, perpindahan yang dilakukan anak tersebut dari posisi awal .....
B. 14 meter arah selatan
C. 10 meter arah tenggara
D. 6 meter arah timur
E. 5 meter arah tenggara
Jawab :
Coba kalian perhatikan sketsa perjalanan yang ditempuh berikut ini :
Besarnya perpindahan dapat dihitung dengan mengukur panjang garis yang menghubungkan posisi awal dengan akhir gerak yang dilakukan ( garis merah pada gambar ). Jika kita buat garis bantu ( garis hijau pada gambar ) maka akan terlihat bentuk segitiga siku-siku dengan garis perpindahan sebagai sisi miringnya. Sehingga besarnya perpindahan dapat dihitung dengan rumus Phytagoras :
Jadi besarnya perpindahan adalah 5 m ke arah tenggara ( E ).
A. 3,29 cm
B. 3,19 cm
C. 3,14 cm
D. 3,09 cm
E. 3,00 cm
Jawab :
Jangka sorong terdiri dari dua skala yakni skala utama dan nonius :
Di depan angka nol (0) skala nonius terlihat skala utama menunjukkan 3,10 cm. Kemudian, garis antara skala utama dan nonius bersatu terlihat skala nonius menunjukkan angka 9 yang artinya 0,09 cm. Hasil pengukuran kedua skala digabung sehingga diperoleh tebal balok = 3,19 cm ( B ).
3. Sebutir peluru 20 gram bergerak dengan kecepatan 10 m/s arah mendatar menumbuk balok bermassa 60 gram yang sedang diam di atas lantai. Jika peluru tertahan di dalam balok maka kecepatan balok sekarang adalah.....
A. 1,0 m/s
B. 1,5 m/s
C. 2,0 m/s
D. 2,5 m/s
E. 3,0 m/s
Jawab :
Jika benda "a" dan "b" bertumbukan, akan berlaku hukum kekekalan momentum :
kerangan :
v = kecepatan benda sebelum tumbukan (m/s)
v'= kecepatan benda setelah tumbukan (m/s)
catatan : momentum merupakan besaran vektor sehingga memperhatikan arah. jika benda bergerak ke kanan kecepatannya bernilai positif (+) maka benda yang bergerak ke kiri kecepatannya bernilai negatif (-).
Karena tumbukan antara peluru(p) dan balok(b) menyebabkan keduanya menjadi satu maka massa dan kecepatan setelah tumbukan menjadi satu juga. Selain itu sebelum terjadi tumbukan balok dalam keadaan diam maka mb.vb = 0 (nol). Sehingga rumus kekekalan momentum berubah menjadi :
keterangan :
mp = massa peluru = 20 g = 2.10-2 kg
mb = massa balok = 60 g = 6.10-2 kg
vp = kecepatan peluru sebelum tumbukan = 10 m/s
v'p.b = kecepatan gabungan peluru dan balok setelah tumbukan (m/s)
Jadi jawabannya adalah 2,5 m/s ( D ).
A. 3 : 2
B. 3 : 1
C. 2 : 1
D. 2 : 3
E. 1 : 3
Jawab :
Hukum kekekalan energi mekanik menyatakan bahwa gabungan energi potensial (Ep) dan energi kinetik (Ek) benda dalam setiap lintasan gerak benda adalah tetap :
Kecepatan benda di posisi A = 0 m/s maka energi kinetik di posisi A (EkA) = 0. Dan rumus energi potensial (Ep) = m.g.h. Rumus di atas menjadi :
5. Tiga buah pegas A, B dan C yang identik dirangkai seperti gambar di bawah !
A. 200 N/m
B. 240 N/m
C. 300 N/m
D. 360 N/m
E. 400 N/m
Jawab :
Diketahui :F = gaya beban = 1,2 N
∆x = pertambahan panjang = 0,6 cm = 0,6 . 10-2 m
Pegas identik berarti besar koinstanta pegasnya sama = k
kemudian, besar konstanta gabungannya dihitung secara bertahap. Pertama kita gabung konstanta pegas bagian atas secara paralel (kp). Lalu hasilnya kita gabung dengan pegas bawahnya secara seri (ks).
Penggabungan secara paralel berarti langsung dijumlahkan :
Penggabungan secara seri dalam bentuk sepernya baru dijumlahkan :
konstanta total (kt) = ks :
Rumus gaya pegas :
Nilai konstanta tiap-tiap pegas ( k ) adalah 300 N/m ( C ).
6. Karet yang panjangnya L digantungkan beban sedemikian rupa sehingga diperoleh data seperti pada tabel :
berdasarkan tabel tersebut, dapat disimpulkan besar konstanta pegas adalah.....
A. 250 N/m
B. 360 N/m
C. 400 N/m
D. 450 N/m
E. 480 N/m
Jawab :
Yang perlu kalian fahami disini adalah beban ( w ) sama dengan gaya ( F ) maka satuannya sama-sama Newton (N) dan ∆l sama artinya dengan ∆x yakni pertambahan panjang. maka soal di atas dapat dikerjakan dengan rumus :
ingat pertambahan panjang harus dalam satuan meter :
∆x = 0,5 cm = 0,005 m
6. Karet yang panjangnya L digantungkan beban sedemikian rupa sehingga diperoleh data seperti pada tabel :
berdasarkan tabel tersebut, dapat disimpulkan besar konstanta pegas adalah.....
A. 250 N/m
B. 360 N/m
C. 400 N/m
D. 450 N/m
E. 480 N/m
Jawab :
Yang perlu kalian fahami disini adalah beban ( w ) sama dengan gaya ( F ) maka satuannya sama-sama Newton (N) dan ∆l sama artinya dengan ∆x yakni pertambahan panjang. maka soal di atas dapat dikerjakan dengan rumus :
ingat pertambahan panjang harus dalam satuan meter :
∆x = 0,5 cm = 0,005 m
(saya menggunakan data kolom pertama, kalian boleh memilih penyelesaian soal dengan data pada kolom-kolom lainnya)
jadi besarnya konstanta pegas = 400 N/m ( C ).
7. Bola bermassa 0,25 kg ditekan pada pegas dengan gaya F seperti pada gambar. anggap percepatan grafitasinya ( g ) = 10 m/s2. Ketika gaya F dihilangkan, bola terlontar ke atas setinggi h meter. Jika energi untuk melontarkan bola besarnya 1,0 joule, maka tinggi h adalah.......A. 50 cm
B. 40 cm
C. 35 cm
D. 25 cm
E. 15 cm
Jawab :
Pada soal di atas terjadi perubahan energi potensial pegas menjadi energi potensial grafitasi.
Rumus-rumusnya :
Keterangan :
m = massa (Kg)
g = percepatan grafitasi (m/s2) = 10 m/s2
h = ketinggian (m)
F = gaya (N)
∆x = pertambahan panjang pegas (m)
karena besarnya energi potensial pegas sudah diketahui maka rumus energi potensial pegas tidak digunakan :
Jadi ketinggian bola ( h ) = 40 cm ( B ).
